Reconcile All The Things

- Part 1: Climbing Mount Effect - Declarative Code and Effects
- Part 2: Reconcile All The Things - Memoization, Data Flow and Reconciliation
- Part 3: Headless React - Live, Yeet Reduce, No-API, WebGPU
Memoization
If you have a slow function slow(x) in your code, one way to speed it up is to memoize it: you cache the last result inside, so that if it's called again with the same x, you get the same result. If the function is static, this is equivalent to just storing the last input and output in a global variable. If it's dynamic, you can use e.g. a closure as the storage:
let memo = (func) => {
let input = undefined;
let output = undefined;
return (x) => {
// Return same output for same input
if (x === input) return output;
// Store new output for new input
input = x;
output = func(x);
return output;
}
};
let slow = memo((x) => { /*...*/ });
This can only buy you time in small code bases with very limited use cases. As soon as you alternate between e.g. slow(a) and slow(b), your cache is useless. The easy solution is to upgrade to a multi-valued cache, where you can retain the outputs for both a and b. Problem is, now you need to come up with an eviction policy to keep your cache from growing indefinitely. This is also assuming that a and b are immutable values that can be compared, and not e.g. mutable trees, or URLs whose remote content you don't even know.
In garbage collected languages, there is a built-in solution to this, in the form of WeakMap. This is a key/value map that can hold data, but which does not own its keys. This means any record inside will be garbage collected unless another part of the program is also holding on to the same key. For this to work, keys must be objects, not primitive values.
let memo = (func) => {
let cache = new WeakMap();
return (x) => {
// Return same output for cached input
let output = cache.get(x);
if (output !== undefined) return output;
// Store new output for new input
output = func(x);
cache.set(x, output);
return output;
}
};
let slow = memo((x) => { /*...*/ });
If a source object is removed elsewhere in the program, the associated cache disappears. It allows you to blindly hold on to an entire collection of derived data, while writing zero lines of code to invalidate any of it. Actual O(0) work. That is, assuming your xs are immutable. This is similar to what you get with reference counting, except WeakMap can also collect cycles.
Unfortunately, this only works for functions of one argument, because each WeakMap key must be one object. If you wish to memoize (x, y) => {...}, you'd need a WeakMap whose keys are xs, and whose values are WeakMaps whose keys are ys. This would only work well if y changes frequently but x does not.
I think this points to a very useful insight about caching: the reason it's so hard is because caches are normally one of the least informed parts of the entire system. A cache has zero contextual information to make any decisions with: it's the code that's accessing the cache that knows what's going on. If that code decides to drop a key or reference, the cache should always follow. Aside from that, how is it supposed to know?
If we are looking for a better solution for caching results, and resumability of code in general, then that's a pretty big clue. We are not looking for a better cache. We are looking for better ways to create context-specific storage. Then we use the simplest possible memoizer. This is 100% reliable. Stale data problems just go away even though you have hidden caches everywhere, it's wild.
Data Flow Graphs
At this point I should address the elephant in the room. If we're talking about declared computations with input dependencies and cached results, isn't this what data flow graphs are for? Today DFGs are still only used in certain niches. They are well suited for processing media like video or audio, or for designing shaders and other data processing pipelines. But as a general coding tool, they are barely used. Why?
We do have a zoo of various reactive, pure, stream-based, observable things... but almost all the successful ones work through code. Even with visual tools, much of their power comes from the ability to wire up custom scriptable nodes, which contain non-reactive, non-pure, non-observable code.
(x) => {
a = A();
b = B(x);
return C(a, b);
}
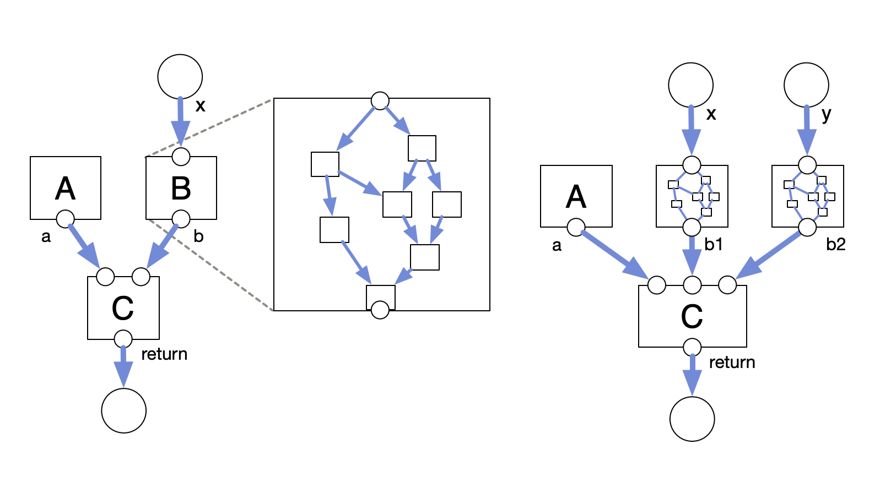
At first it seems like you can trivially take any piece of imperative code and represent it as a DFG. Each function call becomes a node in the graph, and local variables become the edges between function inputs and outputs.
You can also think of a function like B as a sub-graph in a box. It has 1 input and 1 output exposed to the outside in this case.
But there's an important difference between a node in a DFG and a function in a piece of code. In a DFG, each node is a call, not a definition. If you want to call B twice, then you need two unique B nodes, with unique instances of everything inside. You can't just point all the edges to and from the same node.
(x, y) => {
a = A();
b1 = B(x);
b2 = B(y);
return C(a, b1, b2);
}
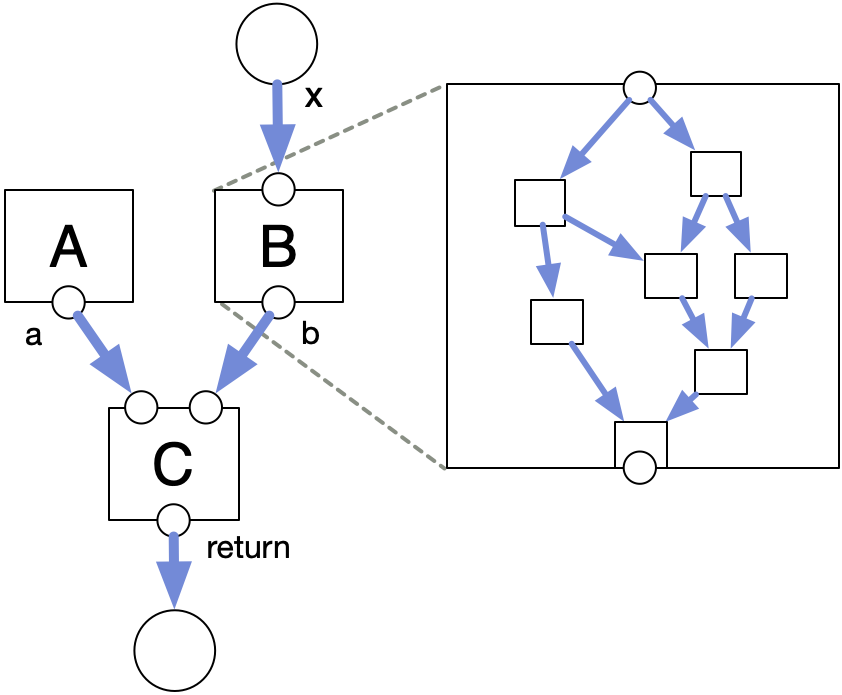
That's because a DFG has no control flow (if/for/while) and no recursion. It represents a stateless computation, without a traditional stack to push and pop. At most you will have e.g. if and match nodes, which select only one of their inputs, as an optimization.
How a DFG is used depends primarily on whether you are editing a DFG or running a DFG. An example of editing a DFG is shader programming: the goal is to write code using a graphical tool. This code will be run on a GPU, applied to each pixel in parallel.
This means the DFG will be transformed into an abstract syntax tree (AST), and compiled down into regular shader code. It's never run directly in its DFG form. If you wish to inspect intermediate results, you need to make a truncated copy of the shader and then run only that.
It is worth noting that this sort of DFG tends to describe computation at a very granular level, i.e. one pixel or audio sample at time, at the very bottom of our program.
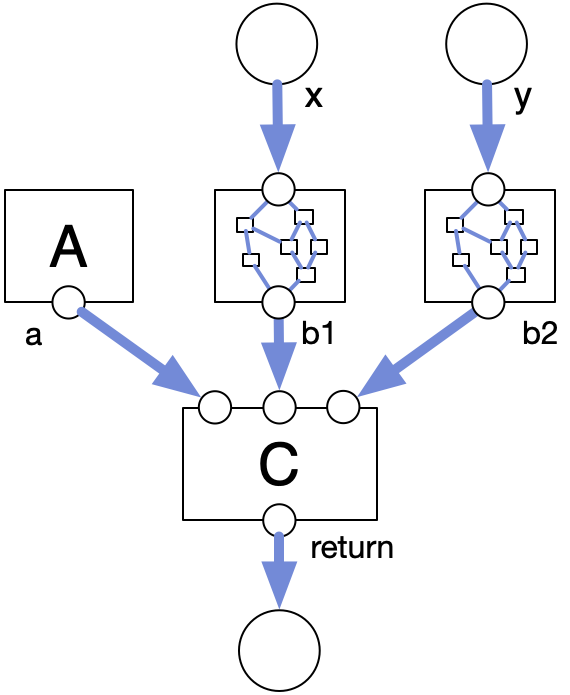
This is all very different from running a live DFG. Here the nodes represent an actual data flow that is being computed. Each edge is a register containing a data value. The values are pushed or pulled through from top to bottom, with intermediate results cached and directly inspectable. This is so the graph can be minimally recomputed in response to changes.
These sorts of graphs tend to operate at the opposite end of the scale, connecting a small number of resources and nodes at the top. An individual edge often carries an entire image or even data set at once, to contain the complexity.
Even then, they get notoriously messy. One reason is that these models often don't have a way to represent a lambda. This causes spaghetti. Think about a piece of code such as:
square = (x) => x * x;
squared = call(square, number);
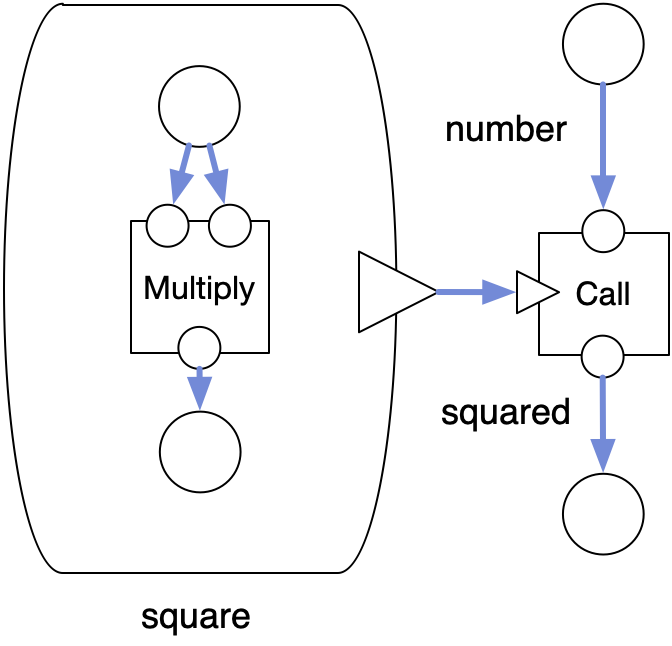
Here, square is not a definition, but a value, which we assign to a variable. We then pass it to the call function, to actually run the lambda. It is possible to represent this in a DFG, and some tools do support this.
We box in a sub-graph like before. However, we don't connect any of the inputs or outputs. Instead there is a special output ▸, which represents a value of type Function, which you can connect to another function-valued input.
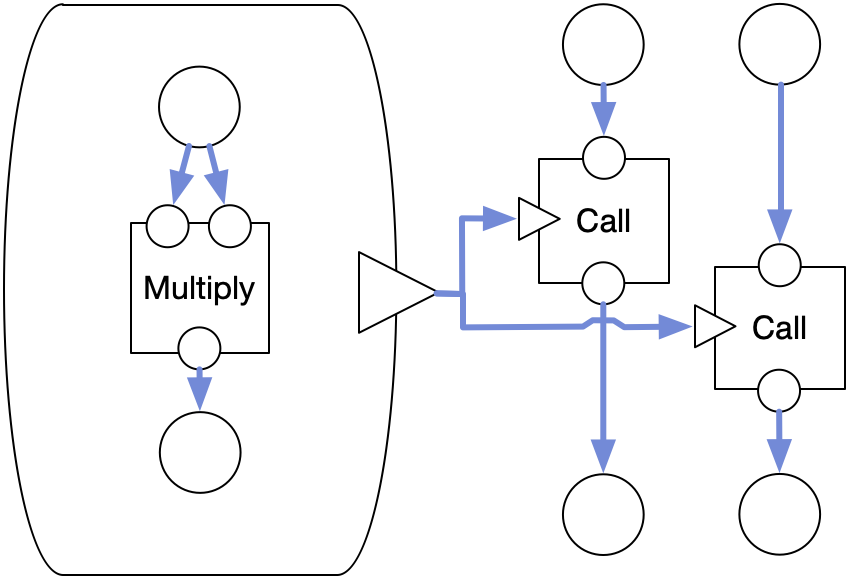
The question is what would happen if you connected the same lambda to two different calls.
This represents a stateless computation, so the two calls happen simultaneously, and need to pass along unique values. This means you need two copies of everything inside the lambda too. So in a live DFG, lambdas don't really provide a Function type but rather a FunctionOnce: a function you may only call once. This is a concept that exists in languages with a notion of ownership, like Rust. If you wish to call it more than once, you need to copy it.
This also means that this does not generalize to N elements. Take for example:
square = (x) => x * x;
numbers = [1, 2, 3, 4]
squared = map(square, numbers);
What would the inside of map look like?
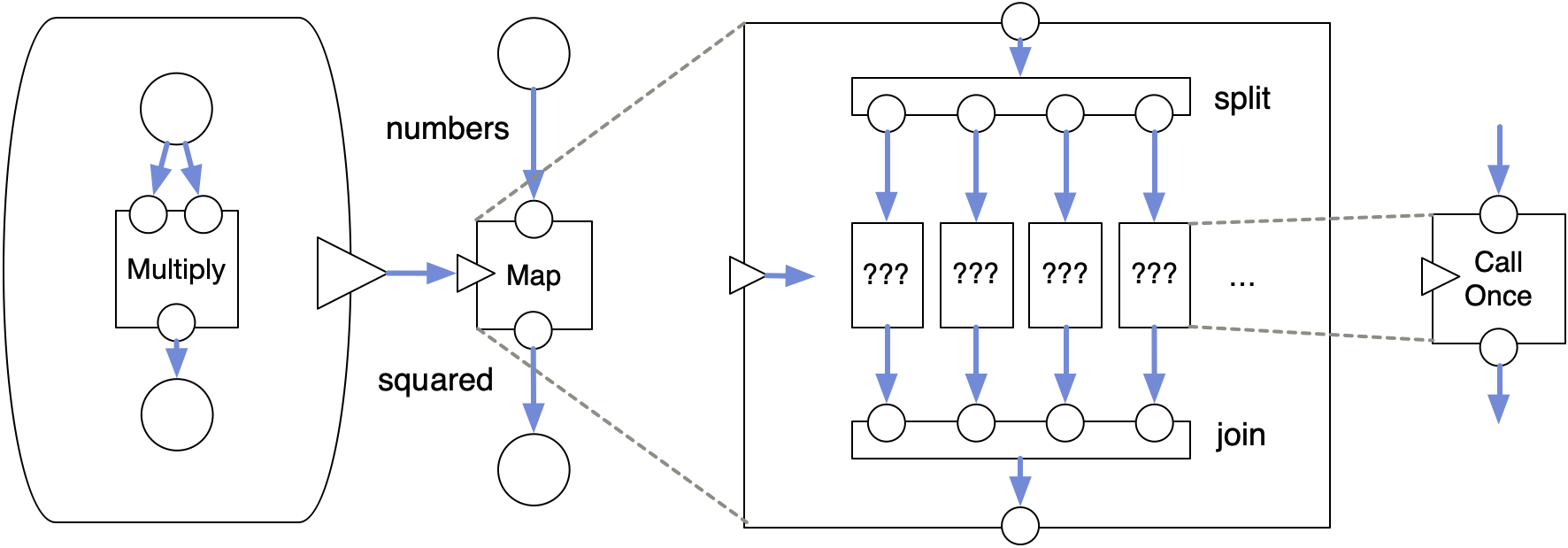
It would need to split the items into individual variables, call the function square on each, and then join them back into a new array. If we add a number to numbers, we would need to add another column, so that we can call the lambda an additional time. If numbers shrinks, the reverse. The DFG must contain N multiply nodes, where N is data-driven and varies at run-time. This is an operation that simply does not exist in a typical DFG environment, at least not as a generic reusable op.
"Scriptable nodes" let you produce any output you like. But they don't let you write code to produce new nodes on the fly. That would mean returning a new piece of DFG instead of a value. You would likely want to attach something to the end so data can flow back to you. If that were possible, it would mean your graph's topology could change freely in response to the data that is flowing through it.
This would have all sorts of implications for maintaining the integrity of data flow. For example, you wouldn't be able to pull data from the bottom of a graph at all if some data at the top changed: you don't even know for sure what the eventual shape will be until you start re-evaluating it in the middle.
Managing a static DFG in memory is pretty easy, as you can analyze its topology once. But evaluating and re-constructing a DFG recursively on the fly is a very different job. If the graph can contain cycles, that's extra hard because now there isn't even a consistent direction of higher or lower anymore.
All this might sound like science fiction but actually it already exists, sort of, almost.
Reconciliation
Here's a simple mock program. We run it twice, once with argument true and once with false. I've lined up the two execution traces to show the matching calls:
let main = (x) => {
A(x);
}
let A = (x) => {
B(x);
D(1);
}
let B = (x) => {
let foo = x ? 3 : 2;
if (x) B(false);
C();
if (x) D(0);
D(foo);
}
let C = () => {};
let D = (x) => {};
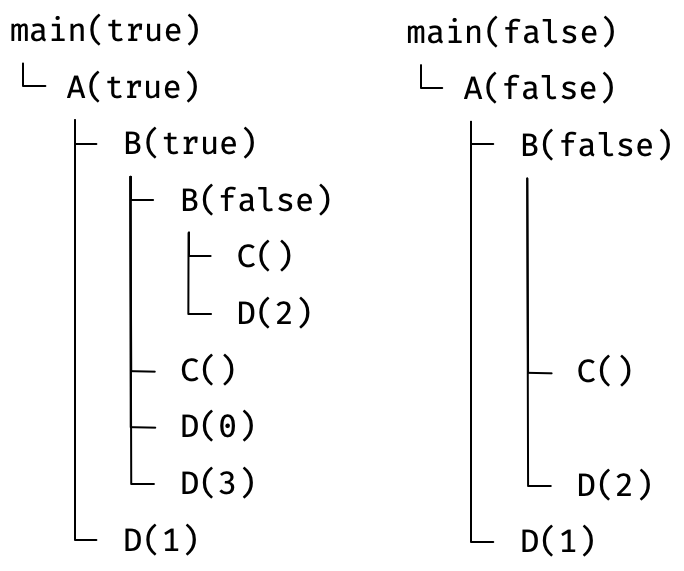
None of these functions return anything, but let's just ignore that for now.
The tree shape shows the evolution of the stack over time. When entering a function, it reserves some space for local variables like foo. When exiting, that space is reclaimed. Any two sibling calls share the same position on the stack, overwriting each other's temporary data. A stack frame can only be identified by its position in the trace's tree, and only exists while a function is running.
Suppose then, that you do record such a trace at run-time. Then when the program is run the second time, you compare at every step, to see if it's making the same calls as before. That would help you with caching.
You can start by trivially matching the initial calls to A and B 1-to-1: only their argument differs. But once you enter B, things change. On the left you have the siblings B(false), C(), D(0), D(3) and on the right you have C(), D(2).
The actual changes are:
- Remove
B(false)and its sub-calls - Remove
D(0) - Replace
D(3)withD(2)
Figuring this out requires you to do a proper minimal diff. Even then, there is ambiguity, because the following would also work:
- Remove
B(false)and its sub-calls - Replace
D(0)withD(2) - Remove
D(3)
From the code you can tell that it should be the former, not the latter. But while this is easy to describe after the fact, it's difficult to imagine how such a thing might actually work at run-time. The only way to know what calls will be made is to run the code. Once you do, it's too late to try and use previous results to save time. Plus, this code only has a few trivial ifs. This becomes even harder if you allow e.g. for loops because now there's a variable number of elements.
In case it's not clear, this is the exact same problem as the live DFG with lambdas in disguise.
We need to introduce the operation of reconciliation: rather than doing work, functions like B must return some kind of data structure that describes the work to be done. Sort of like an effect. Then we can reconcile it with what it returned previously, and map 1-to-1 the calls that are identical. Then we can run it, while reusing cached results that are still valid.
It would also be useful to match calls where only arguments changed, because e.g. B(true) and B(false) share some of the same calls, which can be reused. At least in theory.
Granted, there is a huge constraint here, which the mock scenario obfuscates. Memoizing the calls only makes sense if they return values. But if we passed any returned value into another call, this would introduce a data dependency.
That is, in order to reconcile the following:
let F = (x) => {
let foo = C(x);
D(foo);
if (foo) E();
}
We would need to somehow yield in the middle:
let F = function* (x) {
let foo = C(x);
yield;
D(foo);
if (foo) E();
}
That way we can first reconcile foo = C(x), so we can know whether to reconcile D(false) or D(true), E().
Unfortunately our language does not actually have a trace reconciler built into it, so this can't work. We have two options.
First, we can transpile the code to a deferred form:
let F = function* (x) {
foo = yield call(C)(x)
yield [
call(D)(foo),
foo ? call(E)() : null,
]);
}
Here, call(C)(x) is a value that says we want to call C with the argument x. A deferred function like F returns one or more wrapped calls via a yield. This allows C(x) to be reconciled, obtaining either a cached or fresh value for foo. Then we can reconcile the calls to D(foo) and E().
To make this work would require functions C, D and E to receive the exact same treatment, which we have to be honest, is not a compelling prospect.
Alternatively, we could recognize that C(x) is called first and unconditionally. It doesn't actually need to be reconciled: its presence is always guaranteed if F is called. Let's call such a function a hook.
let F = (x) => {
let foo = C(x);
return defer([
call(D)(foo),
foo ? call(E)() : null
]);
}
If hooks like C(x) aren't reconciled, they're regular function calls, so is all the code inside. Like a scriptable node in a DFG, it's an escape hatch inside the run-time.
But we're also still missing something: actual memoization. While we have the necessary information to reconcile calls across two different executions, we still don't have anywhere to store the memoized state.
So we'll need to reserve some state when we first call F. We'll put all the state inside something called a fiber. We can pass it in as a bound argument to F:
let F = (fiber) => (x) => {
let foo = C(fiber)(x);
return defer([
call(D)(foo),
foo ? call(E)() : null
]);
}
We also pass the fiber to hooks like C: this provides the perfect place for C to store a memoized value and its dependencies. If we run the program a second time and call this exact same F again, in the same place, it will receive the same fiber as before.
As long as the execution flow remains the same between two runs, the fiber and the memoized values inside will remain. Because functions like C are likely to receive exactly the same argument next time, memoization works very well here.
Apropos of nothing, here's how you build a UI component on the web these days:
const Component: React.FC<Props> = (props) => {
const {foo, bar} = props;
// These are hooks, which can only be called unconditionally
const [state, setState] = useState('hello world');
const memoized = useMemo(() => slow(foo), [foo]);
// And there's also something called useEffect
useEffect(() => {
doThing(foo)
return () => undoThing(foo);
}, [foo]);
// Regular JS code goes here
// ...
// This schedules a call to D({foo}) and E()
// They are mounted in the tree inside <Component> recursively
return <>
<D foo={foo} />
{foo ? <E /> : null}
</>
}
It's all there. Though useEffect is a side-show: the real Effects are actually the <JSX> tags, which seem to have all the relevant qualities:
- JSX doesn't run any actual code when we evaluate it
- We can compose multiple JSX elements together in series (nesting) or in parallel (
<>aka "fragments") - The run-time takes care of all the scheduling, mounting and clean up, in the right order
It will reconcile the before and after calls, and preserve the matching fibers, so functions like useMemo can work.
You can also reconcile variable size sets, by returning an array where every call has a key property. This allows minimal diffing in O(N) time.
You may eventually realize that the JSX at the bottom is really just an obscure dialect of JavaScript which lacks a real return statement: what this is returning is not a value at all. It is also not passed back to the parent component but to the run-time. The syntax is optimized for named rather than positional arguments, but that's about it.
What's more, if you do accept these constraints and manage to shoehorn your code into this form, it's strangely not terrible in practice. Often the opposite. Suddenly a lot of complex things that should be hard seem to just fall out naturally. You can actually begin to become 10x. Compared to O(N2) anyway.
The difference with our hypothetical trace reconciler is that there is no way to yield back to a parent during a deferred render. A common work-around in React land is a so-called render prop, whose value is a lambda. The lambda is called by the child during rendering, so it must be entirely side-effect free.
The code:
x = A();
y = B();
z = C(x, y);
must be turned into:
<A>{
(x) => <B>{
(y) => <C x={x} y={y}>{
(z) => {}
}</C>
}</B>
}</A>
This is hideous. Because there is no ability for sibling calls to pass data, B must go inside A, or the other way around. This introduces a false data dependency. But, the data flow graph does match the normal execution trace: in code we also have to decide whether to call A or B first, even if it doesn't matter, unless you explicitly parallelize.
It's interesting that a render prop is an injectable lambda which returns new nodes to mount in the tree. Unlike a "scriptable node", this allows the tree to extend itself on the fly in a Turing-complete yet data-driven way.
So don't think of a reconciler as a tree differ. Think of it as a generalized factory which maintains a perfectly shaped tree of caches called fibers for you. You never need to manually init() or dispose() them... and if you re-run the code in a slightly different way, the fibers that can be re-used will be reused. The value proposition should be pretty clear.
When we made the fiber visible as an argument, much of the magic went away: a React Component is merely a function (fiber) => (props) => DeferredCall. The first argument is implicit, binding it to a unique, persistent fiber for its entire lifetime. The fiber is keyed off the actual call site and the depth in the stack. The hooks can work because they just reserve the next spot in the fiber as each one is called. This is why hooks must be called unconditionally in React: it's only way to keep the previous and next states in sync.
Where we go next is hopefully clear: what if you could use these patterns for things that aren't UI widgets in a tree? Could you retain not just the Effect-like nature, but also the memoization properties? Also, without hideous code? That would be pretty nice.