Making things with Maths
Steven Wittens

 unconed
unconed
http:// acko.net
$$ i\hbar\frac{\partial}{\partial t} \Psi(\mathbf{r},t) = \left [ \frac{-\hbar^2}{2m}\nabla^2 + V(\mathbf{r},t)\right ] \Psi(\mathbf{r},t) $$
“I don’t see how it’s doing society any good
to have its members walking around with
vague memories of algebraic formulas and geometric diagrams, and clear memories of hating them.”
Paul Lockhart, “A Mathematician's Lament”
$$ Area = \frac{b \cdot h}{2} $$
“The power to understand and predict
the quantities of the world should not be restricted to those with a freakish knack for manipulating abstract symbols.”
Bret Victor, “Kill Math”
f=Math; e=document.body.children[$=0]; G="globalCompositeOperation"; Q=.43; P=.05; with(e){ with(style)width=(w=innerWidth-9)+"px", height=(h=innerHeight-25)+"px"; W=(width=w/=2)/2; H=(height=h/=2)/2; g=getContext("2d"); t=w/h} with(g){ scale(W/t,H); translate(t,1); setInterval(function(){ with(E=e.cloneNode(0)) width=height=H, c=getContext("2d"); c.fillRect(0,0,h,h); g[G]=c[G]="lighter"; C=f.cos; S=f.sin; L=f.atan2; q=C($); r=S(q-$*.7)+Q; u=C(r-$*Q)+Q; a=L(q,-u*2); b=L(r,u*u+q*q); n=C(a); o=S(a); N=C(b); O=S(b); $+=P; clearRect(-t,-1,2*t,2); for(i=14; i>4; --i){ v=0; for(j=25; j; ){ M=f.log(j+.2)*Q; j--; _=$-j*.07-i*4; A=C(_+S(_*.8))*2+_*P; B=S(_*.7-C(_*Q))*3; x=C(A)*C(B)*M-q; y=S(A)*C(B)*M-r; z=S(B)*M-u; k=x*n+z*o; _=z*n-x*o; l=y*N+_*O; z=_*N-y*O; lineTo(k/=z,l/=z); lineWidth=P/z; strokeStyle="hsl("+60*S($-z)+",60%,"+~~(40-j)*(Q+!j+(.1>($-j*P)%1))+"%)"; if(z>.1)v++&&stroke(); else{ v=0} beginPath(); moveTo(k,l)} } A="drawImage"; N=H/2; c.globalAlpha=Q; c[A](e,0,0,H,H); X=k*N+N; Y=l*N+N; K=1.1; c.translate(X,Y); while(i--)c.scale(K,K),c[A](E,-X,-Y,H,H); g[A](E,-t,-1,2*t,2)} ,33)}
Background
→
Tip: Hold shift to slow down animations.
$$ y = 0.5 - 0.5 \cdot \cos x $$
$$ r = 0.5 - 0.5 \cdot \cos \theta $$
$$ r = 0.5 + 0.5 \cdot \cos 8 \theta $$
$$ \begin{array}{rl}
r = & \arcsin(0.5 + 0.5 \cos 8 \theta) \\
& ( 0.5 + 0.5 \cos \theta) \\
\end{array} $$
$$ \frac{\partial \mathbf{v}}{\partial t} + \mathbf{v} \cdot \nabla \mathbf{v} = -\frac{1}{\rho} \nabla p + \nu \nabla^2 \mathbf{v} + \mathbf{f} $$
→
$$
y = \frac{x+1}{x-3} \frac{1}{x} \frac{1}{x+2}
$$
→
Math Machines
Bezier Curves


Paul de Casteljau

1959

Pierre Bézier

1962
Vectors
$$ \class{mj-blue}{\vec a} $$
$$ \class{mj-blue}{\vec a} , \class{mj-red}{\vec b} $$
$$ \class{mj-blue}{\vec a} = \class{mj-red}{\vec b} $$
$$ \class{mj-blue}{\vec a} \neq \class{mj-red}{\vec b} $$
$$ \class{mj-blue}{\vec a} + \class{mj-red}{\vec b} = \class{mj-green}{\vec c} $$
$$ \class{mj-green}{\vec c} - \class{mj-red}{\vec b} = \class{mj-blue}{\vec a} $$
$$ \class{mj-blue}{\vec a} + \class{mj-blue}{\vec a} + \class{mj-blue}{\vec a} = 3 \cdot \class{mj-blue}{\vec a} = \class{mj-green}{\vec b} $$
$$ \class{mj-blue}{\vec a} = \frac{\class{mj-green}{\vec b}}{3} = \frac{1}{3} \cdot \class{mj-green}{\vec b} $$
$$ \class{mj-red}{\vec b} - \class{mj-blue}{\vec a} = \class{mj-green}{\vec c} $$
$$ \class{mj-purple}{\vec d} = \class{mj-blue}{\vec a} + \frac{1}{3} \cdot (\class{mj-red}{\vec b} - \class{mj-blue}{\vec a}) $$
Linear interpolation
$$ lerp({\vec a}, {\vec b}, t) = \vec a + t \cdot (\vec b - \vec a) $$Quadratic Bezier Curve
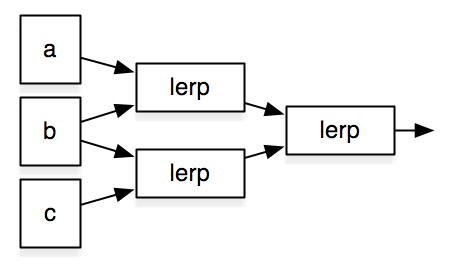
Cubic Bezier Curve
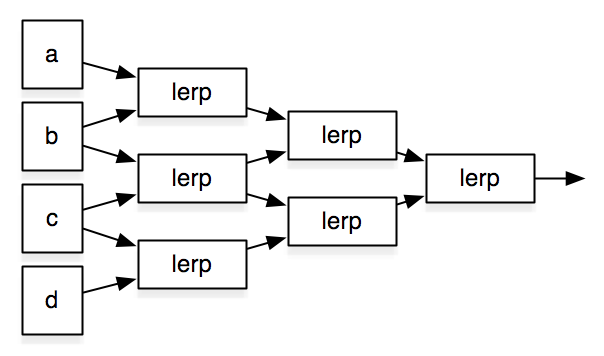
Bicubic Bezier Surface

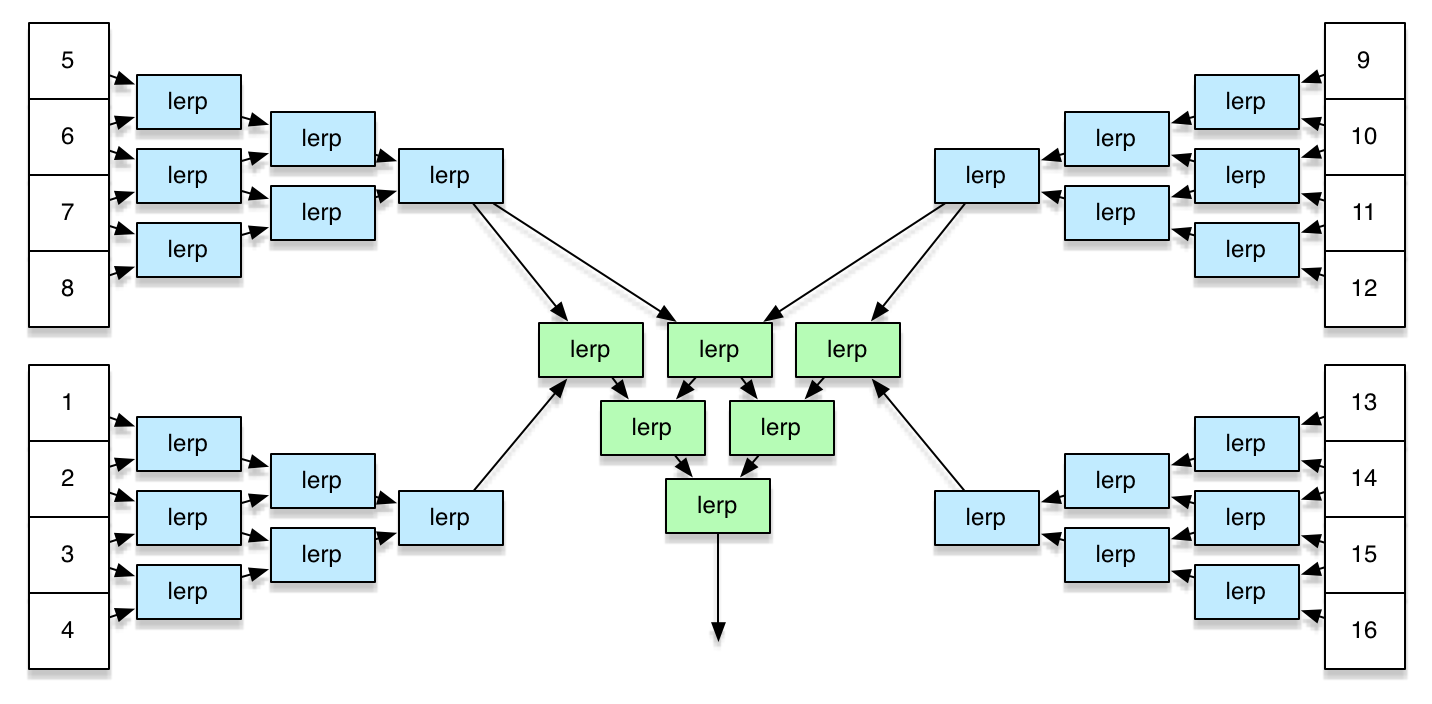
Procedural Generation
Iñigo Quilez, Pixar
“To make a film, we have to direct
almost 200 billion pixels.
That's a lot of mathematics.”









→
→
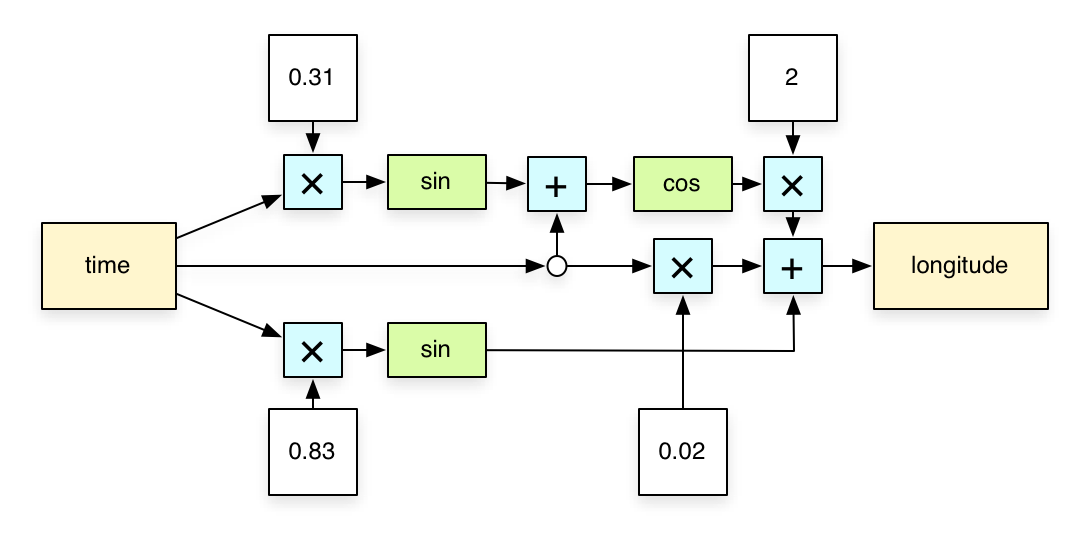
Longitude
Latitude
longitude = cos(time + sin(time * 0.31)) * 2 + sin(time * 0.83) * 3 + time * 0.02 latitude = sin(time * 0.7 + 1) - cos(3 + time * 0.43 + sin(time) * 0.13) * 2.3
$$ x $$
$$ x =\hspace{3 pt}? $$
function (x) { return x }
$$ x = $$
$$ \ldots $$
$$ -4 $$
$$ -3 $$
$$ -2 $$
$$ -1 $$
$$ 0 $$
$$ 1 $$
$$ 2 $$
$$ 3 $$
$$ 4 $$
$$ \ldots $$
$$ f(x) = x $$
$$ f(x) = 1 $$
$$ f(x) = 2x $$
$$ f(x) = 2x + 1 $$
$$ f(x) = \left|2x + 1\right| $$
$$ f(x) = \left| 2x + 1 \right| - 4 $$
$$ f(x) = \left| \left| 2x + 1 \right| - 4 \right| $$
$$ f(x) = \left| \left| 2x + 1 \right| - 4 \right| - 2.5 $$
$$ f(x) = \left| \left| \left| 2x + 1 \right| - 4 \right| - 2.5 \right| $$
$$ \class{mj-blue}{f(x) = 2.5 \cdot \arctan x} $$
$$
\class{mj-green}{g(x) = x}
$$
$$ \class{mj-blue}{f(x) = 2.5 \cdot \arctan x} $$
$$ \class{mj-green}{g(x) = \sin 6x} $$
$$ \class{mj-red}{f(x) + g(x)} $$
$$
\class{mj-blue}{ f(x) = 0.5 + 0.5 \cdot \cos x }
$$
$$
\class{mj-blue}{ f(x) = 0.5 + 0.5 \cdot \cos ( max(-\pi, min(\pi, x))) }
$$
$$
\class{mj-blue}{ f(x) = 0.5 + 0.5 \cdot \cos ( max(-\pi, min(\pi, x))) } $$
$$
\class{mj-green}{ g(x) = thing(x, t) }
$$
$$
\class{mj-blue}{ f(x) = 0.5 + 0.5 \cdot \cos ( max(-\pi, min(\pi, x))) } $$
$$
\class{mj-red}{ g(x) = f(x) \cdot thing(x, t) }
$$
→
Stacked Value Noise

Physics
$$ \class{mj-blue}{\vec p} $$
$$ \class{mj-blue}{\vec p}, \class{mj-green}{\vec v} $$
$$ \class{mj-blue}{\vec p_1} = \class{mj-blue}{\vec p_0} + \class{mj-green}{\vec v_0} \cdot 1 s $$
$$ \class{mj-blue}{\vec p_{1.5}} = \class{mj-blue}{\vec p_1} + \class{mj-green}{\vec v_1} \cdot 0.5 s $$
$$ \class{mj-blue}{\vec p_{i+1}} = \class{mj-blue}{\vec p_i} + \class{mj-green}{\vec v_i} \cdot \Delta t $$
$$ \vec f = \ldots $$
$$ \class{mj-red}{\vec a} = \frac{\vec f}{m} $$
$$ \class{mj-blue}{\vec p_{i+1}} = \class{mj-blue}{\vec p_i} + \class{mj-green}{\vec v_i} \cdot \Delta t $$
$$ \class{mj-blue}{\vec p_{i+1}} = \class{mj-blue}{\vec p_i} + \class{mj-green}{\vec v_i} \cdot \Delta t $$
$$ \class{mj-green}{\vec v_{i+1}} = \class{mj-green}{\vec v_i} + \class{mj-red}{\vec a_i} \cdot \Delta t $$
Euler integration
$$ f = -k \cdot x $$
→
→
$$ \class{mj-blue}{\vec p_{i+1}} = \class{mj-blue}{\vec p_i} + \class{mj-green}{\vec v_i} \cdot \Delta t \\
\class{mj-green}{\vec v_{i+1}} = \class{mj-green}{\vec v_i} + \class{mj-red}{\vec a_i} \cdot \Delta t $$
$$ \vec p_{i+1} = \vec p_{i} + \int_T^{T + \Delta t}{\vec v(t) \cdot dt} $$
$$ ????? $$
$$ ????? $$
Verlet Integration
Runge-Kutta Methods
$$ O(\Delta t) \\ O(\Delta t^2) \\ O(\Delta t^3) $$
Runge-Kutta Methods
$$ O(\Delta t) \\ O(\Delta t^2) \\ O(\Delta t^3) $$
Sandboxes and Toys
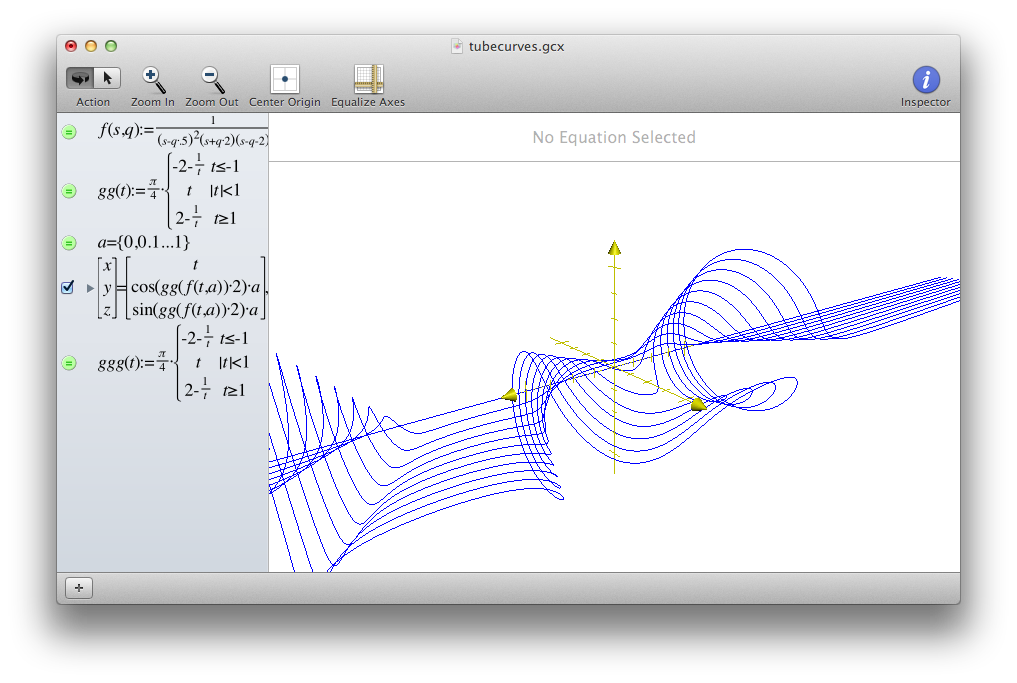
Grapher.app (OS X)
MandelBulber.com — 3D Fractal Explorer

GLSL Sandbox, ShaderToy, Processing(.js)
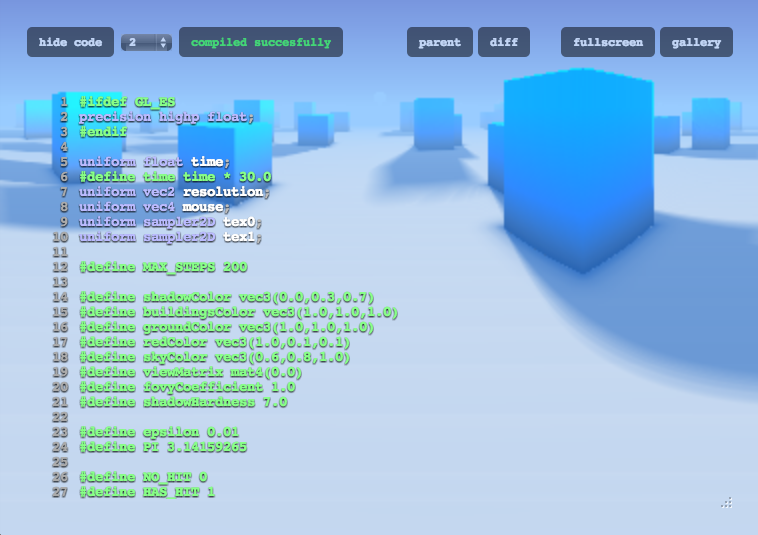
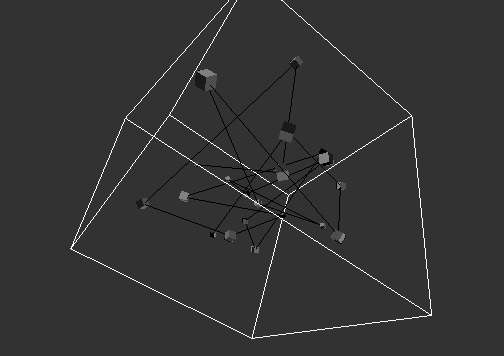

(Web) Audio, AI, Puzzles

3D Printing, Electronics, Arduino


References
Nature Of Code.com — Daniel Shiffman

“Doodling in Math Class” — Vihart
YouTube.com / user / Vihart



“Kill Math” — Bret Victor
Worry Dream.com / KillMath

Better Explained.com
Thanks! – More Like This
“How to Fold a Julia Fractal”
“To Infinity And Beyond”


Acko.net – Slides powered by MathBox.js