
Yak Shading
Data-Driven Geometry
MathBox primitives need to take arbitrary data, transform it on the fly, and render it as styled geometry based on their attributes. Done as much as possible on the graphics hardware.
Three.js can render points, lines, triangles, but only with a few predetermined strategies. The alternative is to write your own vertex and fragment shader and do everything from scratch. Each new use case means a new ShaderMaterial with its own properties, so called uniforms. If the stock geometry doesn't suffice, you can make your own triangles by filling a raw BufferGeometry and assign custom per-vertex attributes. Essentially, to leverage GPU computation with Three.js—most engines, really—you have to ignore most of it.
Virtual Geometry
Shader computations are mainly rote transforms. For example, if you want to draw a line between two points, you'll have to make a long rectangle, made out of two triangles. But this simple idea gets complicated quickly once you add corner joins, depth scaling, 3D clipping, and so on. Doing this to an entire data set at once is what GPUs are made for, through vertex shaders which transform points.

Vertex shaders can only do 1-to-1 mappings. This isn't a problem by itself. You can use a gather approach to do N-to-1 mapping, where all the necessary data is pre-arranged into attribute arrays, with the data repeated and interleaved per vertex as necessary.
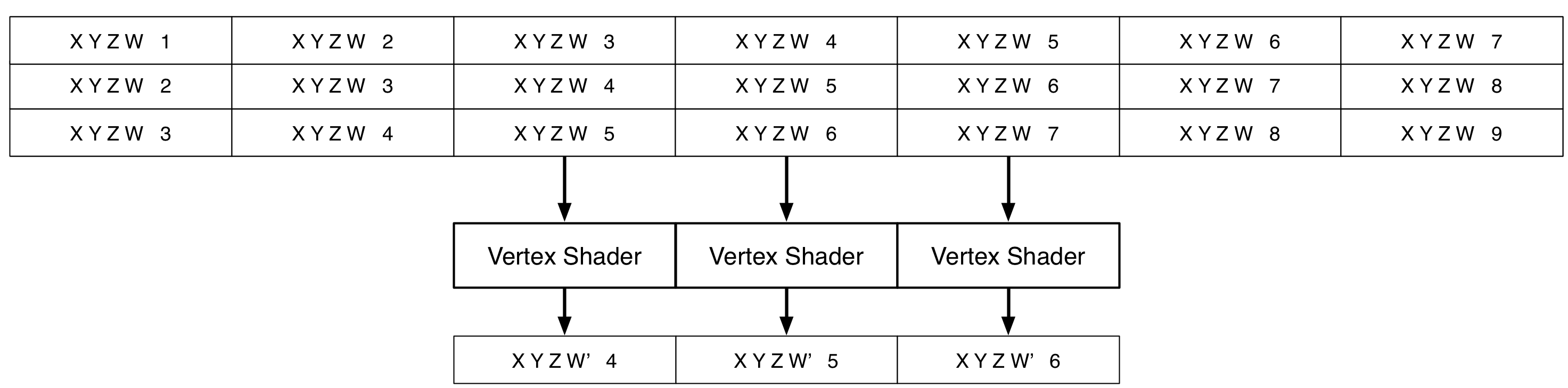
The proper tool for this is a geometry shader: a program that creates new geometry by N-to-M mapping of data, like making triangles out of points. WebGL doesn't support geometry shaders, won't any time soon, but you can emulate them with texture samplers. A texture image is just a big typed array, and you have random access unlike vertex attributes.
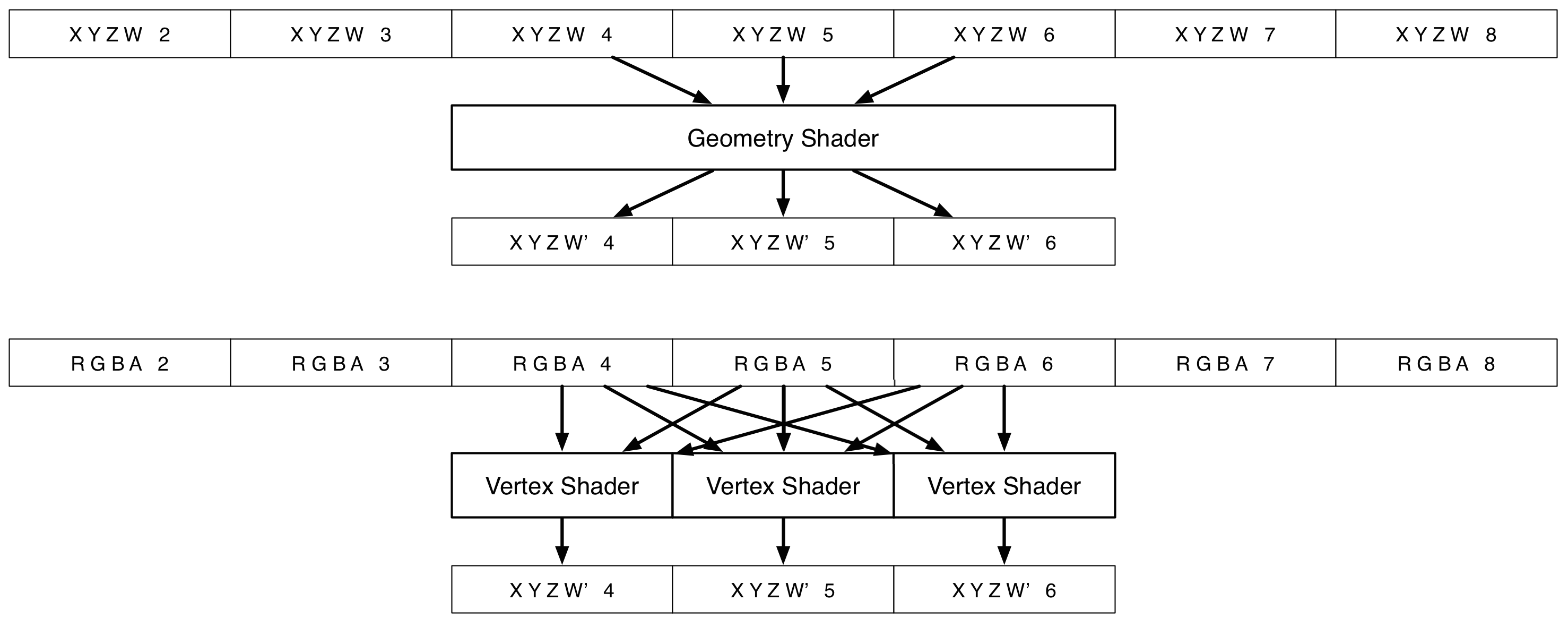
The original geometry acts only as a template, directing the shader's real data lookups. You lose some performance this way, but it's not too bad. Any procedural sampling pattern works, drawing 1 shape or 10,000. As textures can be rendered to, not just from, this also enables transform feedback, using the result of one pass to create new geometry in another.
All geometry rendered this way is 100% static as far as Three.js is concerned. New values are uploaded directly to GPU memory just before the rendering starts. The only gotcha is handling variable size input, because reallocation is costly. Pre-allocating a larger texture is easy, but clipping off the excess geometry in an O(1) fashion on the JS side is hard. In most cases there's the work around of dynamically generating degenerate triangles in a shader, which collapse down to invisible edges or points. This way, MathBox can accept variable sized arrays in multiple dimensions and will do its best to minimize disruption. If attribute instancing was more standard in WebGL, this wouldn't be such an issue, but as it stands, the workarounds are very necessary.
Vertex Party
If you squint very hard it looks a bit like React for live geometry. Except instead of a diffing algorithm, there's a few events, some texture uploads, a handful of draw calls and then an idle CPU. It's ideal for drawing thousands of things that look similar and follow the same rules. It can handle not just basic GL primitives like lines or triangles, but higher level shapes like 3D arrows or sprites.
My first prototype of this was my last christmas demo. It was messy and tedious to make, especially the shaders, but it performed excellently: the final scene renders ~200,000 triangles. Despite being a layer around Three.js … around WebGL … around OpenGL … around a driver … around a GPU … performance has far exceeded my expectations. Even complex scenes run great on my Android phone, easily 10x faster than MathBox 1, in some cases more like 1000x.
Of course compared to cutting edge DirectX or OpenCL (not a typo), this is still very limited. In today's GPUs, the charade of attributes, geometries, vertices and samples has mostly been stripped away. What remains is buffers and massive operations on them, exposed raw in new APIs like AMD's Mantle and iOS's Metal. My vertex trickery acts like a polyfill, virtualizing WebGL's capabilities to bring them closer to the present. It goes a bit beyond what geometry shaders can provide, but still lacks many useful things like atomic append queues or stream compaction.
For large geometries, the set up cost can be noticeable though. Shader compilation time also grows with transform complexity, doubly so on Windows where shaders are recompiled to HLSL / Direct3D. This makes drawing ops the heaviest MathBox primitives to spawn and reallocate. You could call this the MathBox version of the dreaded 'paint' of HTML. Once warmed up though, most other properties can be animated instantly, including the data being displayed: this is the opposite of how HTML works. Hence you can mostly spawn things ahead of time, revealing and hiding objects as needed, with minimal overhead and jank at runtime.
This all relies on carefully constructed shaders which have to be wired up in all their individual permutations. This needed to be solved programmatically, which is where we go last.
- MathBox² - PowerPoint Must Die
- A DOM for Robots - Modelling Live Data
- Yak Shading - Data Driven Geometry
- ShaderGraph 2 - Functional GLSL