To Infinity… And Beyond!
Exploring the outer limits
“It is known that there are an infinite number of worlds, simply because there is an infinite amount of space for them to be in. However, not every one of them is inhabited. Therefore, there must be a finite number of inhabited worlds.
Any finite number divided by infinity is as near to nothing as makes no odds, so the average population of all the planets in the universe can be said to be zero. From this it follows that the population of the whole universe is also zero, and that any people you may meet from time to time are merely the products of a deranged imagination.”– The Restaurant at the End of the Universe, Douglas Adams
If there's one thing mathematicians have a love-hate relationship with, it has to be infinity. It's the ultimate tease: it beckons us to come closer, but never allows us anywhere near it. No matter how far we travel to impress it, infinity remains disinterested, equally distant from everything: infinitely far!
$$ 0 < 1 < 2 < 3 < … < \infty $$
Yet infinity is not just desirable, it is absolutely necessary. All over mathematics, we find problems for which no finite amount of steps will help resolve them. Without infinity, we wouldn't have real numbers, for starters. That's a problem: our circles aren't round anymore (no $ π $ and $ \tau $) and our exponentials stop growing right (no $ e $). We can throw out all of our triangles too: most of their sides have exploded.
A steel railroad bridge with a 1200 ton counter-weight.
Completed in 1910. Source: Library of Congress.
We like infinity because it helps avoid all that. In fact even when things are not infinite, we often prefer to pretend they are—we do geometry in infinitely big planes, because then we don't have to care about where the edges are.
Now, suppose we want to analyze a steel beam, because we're trying to figure out if our proposed bridge will stay up. If we want to model reality accurately, that means simulating each individual particle, every atom in the beam. Each has its own place and pushes and pulls on others nearby.
But even just $ 40 $ grams of pure iron contains $ 4.31 \cdot 10^{23} $ atoms. That's an inordinate amount of things to keep track of for just 1 teaspoon of iron.
Instead, we pretend the steel is solid throughout. Rather than being composed of atoms with gaps in between, it's made of some unknown, filled in material with a certain density, expressed e.g. as grams per cubic centimetre. Given any shape, we can determine its volume, and hence its total mass, and go from there. That's much simpler than counting and keeping track of individual atoms, right?
Unfortunately, that's not quite true.
The Shortest Disappearing Trick Ever
Like all choices in mathematics, this one has consequences we cannot avoid. Our beam's density is mass per volume. Individual points in space have zero volume. That would mean that at any given point inside the beam, the amount of mass there is $ 0 $. How can a beam that is entirely composed of nothing be solid and have a non-zero mass?
Bam! No more iron anywhere.
While Douglas Adams was being deliberately obtuse, there's a kernel of truth there, which is a genuine paradox: what exactly is the mass of every atom in our situation?
To make our beam solid and continuous, we had to shrink every atom down to an infinitely small point. To compensate, we had to create infinitely many of them. Dividing the finite mass of the beam between an infinite amount of atoms should result in $ 0 $ mass per atom. Yet all these masses still have to add up to the total mass of the beam. This suggests $ 0 + 0 + 0 + … > 0 $, which seems impossible.
If the mass of every atom were not $ 0 $, and we have infinitely many points inside the beam, then the total mass is infinity times the atomic mass $ m $. Yet the total mass is finite. This suggests $ m + m + m + … < \infty $, which also doesn't seem right.
It seems whatever this number $ m $ is, it can't be $ 0 $ and can't be non-zero. It's definitely not infinite, we only had a finite mass to begin with. It's starting to sound like we'll have to invent a whole new set of numbers again to even find it.
That's effectively what Isaac Newton and Gottfried Leibniz set in motion at the end of the 17th century, when they both discovered calculus independently. It was without a doubt the most important discovery in mathematics and resulted in formal solutions to many problems that were previously unsolvable— our entire understanding of physics has relied on it since. Yet it took until the late 19th century for the works of Augustin Cauchy and Karl Weierstrass to pop up, which formalized the required theory of convergence. This allows us to describe exactly how differences can shrink down to nothing as you approach infinity. Even that wasn't enough: it was only in the 1960s when the idea of infinitesimals as fully functioning numbers—the hyperreal numbers—was finally proven to be consistent enough by Abraham Robinson.
But it goes back much further. Ancient mathematicians were aware of problems of infinity, and used many ingenious ways to approach it. For example, $ π $ was found by considering circles to be infinite-sided polygons. Archimedes' work is likely the earliest use of indivisibles, using them to imagine tiny mechanical levers and find a shape's center of mass. He's better known for running naked through the streets shouting Eureka! though.
That it took so long shows that this is not an easy problem. The proofs involved are elaborate and meticulous, all the way back. They have to be, in order to nail down something as tricky as infinity. As a result, students generally learn calculus through the simplified methods of Newton and Leibniz, rather than the most mathematically correct interpretation. We're taught to mix notations from 4 different centuries together, and everyone's just supposed to connect the dots on their own. Except the trail of important questions along the way is now overgrown with jungle.
Still, it shows that even if we don't understand the whole picture, we can get a lot done. This article is in no way a formal introduction to infinitesimals. Rather, it's a demonstration of why we might need them.
What is happening when we shrink atoms down to points? Why does it make shapes solid yet seemingly hollow? Is it ever meaningful to write $ x = \infty $? Is there only one infinity, or are there many different kinds?
To answer that, we first have to go back to even simpler times, to Ancient Greece, and start with the works of Zeno.
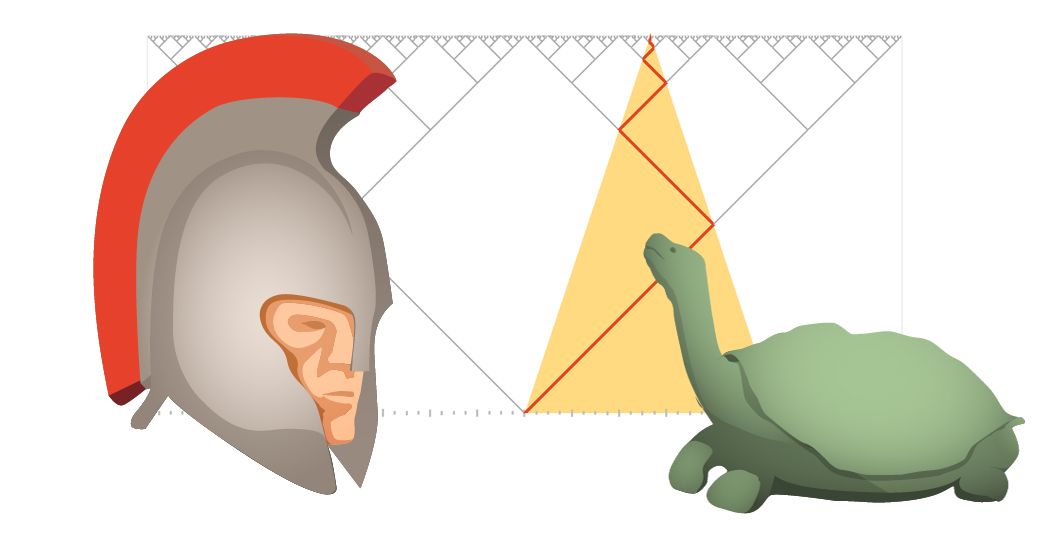
Achilles and the Tortoise
Zeno of Elea was one of the first mathematicians to pose these sorts of questions, effectively trolling mathematics for the next two millennia. He lived in the 5th century BC in southern Italy, although only second-hand references survive. In his series of paradoxes, he examines the nature of equality, distance, continuity, of time itself.
Because it's the ancient times, our mathematical knowledge is limited. We know about zero, but we're still struggling with the idea of nothing. We've run into negative numbers, but they're clearly absurd and imaginary, unlike the positive numbers we find in geometry. We also know about fractions and ratios, but square roots still confuse us, even though our temples stay up.
Limits are the first tool in our belt for tackling infinity. Given a sequence described by countable steps, we can attempt to extend it not just to the end of the world, but literally forever. If this works we end up with a finite value. If not, the limit is undefined. A limit can be equal to $ \infty $, but that's just shorthand for the sequence has no upper bound. Negative infinity means no lower bound.
Breaking Away From Rationality
Until now we've only encountered fractions, that is, rational numbers. Each of our sums was made of fractions. The limit, if it existed, was also a rational number. We don't know whether this was just a coincidence.
It might seem implausible that a sequence of numbers that is 100% rational and converges, can approach a limit that isn't rational at all. Yet we've already seen similar discrepancies. In our first sequence, every partial sum was less than $ 1 $. Meanwhile the limit of the sum was equal to $ 1 $. Clearly, the limit does not have to share all the properties of its originating sequence.
We also haven't solved our original problem: we've only chopped things up into infinitely many finite pieces. How do we get to infinitely small pieces? To answer that, we need to go looking for continuity.
Generally, continuity is defined by what it is and what its properties are: a noticeable lack of holes, and no paradoxical values. But that's putting the cart before the horse. First, we have to show which holes we're trying to plug.
What we just did was a careful exercise in hiding the obvious, namely the digit-based number systems we are all familiar with. By viewing them not as digits, but as paths on a directed graph, we get a new perspective on just what it means to use them. We've also seen how this means we can construct the rationals and reals using the least possible ingredients required: division by two, and limits.
Drowning By Numbers
In school, we generally work with the decimal representation of numbers. As a result, the popular image of mathematics is that it's the science of digits, not the underlying structures they represent. This permanently skews our perception of what numbers really are, and is easy to demonstrate. You can google to find countless arguments of why $ 0.999… $ is or isn't equal to $ 1 $. Yet nobody's wondering why $ 0.000… = 0 $, though it's practically the same problem: $ 0.1, 0.01, 0.001, 0.0001, … $
Furthermore, in decimal notation, rational numbers and real numbers look incredibly alike: $ 3.3333… $ vs $ 3.1415…\, $ The question of what it actually means to have infinitely many non-repeating digits, and why this results in continuous numbers, is hidden away in those 3 dots at the end. By imagining $ π $ as $ 3.1415…0000… $ or $ 3.1415…1111… $ we can intuitively bridge the gap to the infinitely small. We see how the distance between two neighbouring real numbers must be so small, that it really is equivalent to $ 0 $.
That's not as crazy as it sounds. In the field of hyperreal numbers, every number actually has additional digits 'past infinity': that's its infinitesimal part. You can imagine this to be a multiple of $ \frac{1}{\infty} $, an infinitely small unit greater than $ 0 $, which I'll call $ ε $. You can add $ ε $ to a real number to take an infinitely small step. It represents a difference that can only be revealed with an infinitely strong microscope. Equality is replaced with adequality: being equal aside from an infinitely small difference.
You can explore this hyperreal number line below.
As $ ε $ is a fully functioning hyperreal number, $ ε^2 $ is also infinitesimal. In fact, it's even infinitely smaller than $ ε $, and we can keep doing this for $ ε^3, ε^4, …\,$ To make matters worse, if $ ε $ is infinitesimal, then $ \frac{1}{ε} $ must be infinitely big, and $ \frac{1}{ε^2} $ infinitely bigger than that. So hyperreal numbers don't just have inwardly nested infinitesimal levels, but outward levels of increasing infinity too. They have infinitely many dimensions of infinity both ways.
So it's perfectly possible to say that $ 0.999… $ does not equal $ 1 $, if you mean they differ by an infinitely small amount. The only problem is that in doing so, you get much, much more than you bargained for.
A Tug of War Between the Gods
That means we can finally answer the question we started out with: why did our continuous atoms seemingly all have $ 0 $ mass, when the total mass was not $ 0 $? The answer is that the mass per atom was infinitesimal. So was each atom's volume. The density, mass per volume, was the result of dividing one infinitesimal amount by another, to get a normal sized number again. To create a finite mass in a finite volume, we have to add up infinitely many of these atoms.
These are the underlying principles of calculus, and the final puzzle piece to cover. The funny thing about calculus is, it's conceptually easy, especially if you start with a good example. What is hard is actually working with the formulas, because they can get hairy very quickly. Luckily, your computer will do them for you:
That was differential and integral calculus in a nutshell. We saw how many people actually spend hours every day sitting in front of an integrator: the odometers in their cars, which integrate speed into distance. And the derivative of speed is acceleration—i.e. how hard you're pushing on the gas pedal or brake, combined with forces like drag and friction.
By using these tools in equations, we can describe laws that relate quantities to their rates of change. Drag, also known as air resistance, is a force which gets stronger the faster you go. This is a relationship between the first and second derivatives of position.
In fact, the relaxation procedure we applied to our track is equivalent to another physical phenomenon. If the curve of the coaster represented the temperature along a thin metal rod, then the heat would start to equalize itself in exactly that fashion. Temperature wants to be smooth, eventually averaging out completely into a flat curve.
Whether it's heat distribution, fluid dynamics, wave propagation or a head bobbing in a roller coaster, all of these problems can be naturally expressed as so called differential equations. Solving them is a skill learned over many years, and some solutions come in the form of infinite series. Again, infinity shows up, ever the uninvited guest at the dinner table.
Closing Thoughts
Infinity is a many splendored thing but it does not lift us up where we belong. It boggles our mind with its implications, yet is absolutely essential in math, engineering and science. It grants us the ability to see the impossible and build new ideas within it. That way, we can solve intractable problems and understand the world better.
What a shame then that in pop culture, it only lives as a caricature. Conversations about infinity occupy a certain sphere of it—Pink Floyd has been playing on repeat, and there's usually someone peddling crystals and incense nearby.
"Man, have you ever, like, tried to imagine infinity…?" they mumble, staring off into the distance.
"Funny story, actually. We just came from there…"
Comments, feedback and corrections are welcome on Google Plus. Diagrams powered by MathBox.
More like this: How to Fold a Julia Fractal.
